top of page

CARACTÉRISTIQUES ET PROPRIÉTÉS DES SOLIDES CRISTALLINS

 

 

Symétrie d'ordre n

Dire qu'un objet possède une symétrie d’ordre n autour d’un axe (d) signifie que toute rotation d’angle 2π/n autour de l’axe (d) laisse cet objet globalement invariant. Les flocons de neige sont des exemples assez éloquents de ce type de symétrie

 

         Le motif géométrique élémentaire du pavage (dont les sommets sont des atomes ou plus souvent des ions) est appelé réseau. Il existe un nombre restreint de réseaux pouvant remplir l’espace par translations périodiques: il a été prouvé que ces réseaux ne peuvent posséder que des symétries d’ordre 2, 3, 4 ou 6.

 

     Il n'existe que quatorze possibilités de motifs pouvant constituer un pavage capable de remplir un espace en trois dimensions. On peut classer ces motifs en sept groupes selon la norme des vecteurs de translations et les angles que ces derniers définissent. C'est Auguste Bravais qui, en 1848, fut le premier à classer les réseaux cristallins de la sorte, d'où leur nom: réseaux de Bravais.

          La notion de maille cristalline est relativement proche de celle du réseau de bravais : la différence réside dans le fait que le réseau représente un motif, alors que la maille montre l’emplacement des atomes (ou des ions) selon ce réseau. De plus il existe une notion de paramètre de maille : cette grandeur rend compte de la distance entre les atomes (ici a, b et c) et des angles entre leurs liaisons (ici α, β, et γ).

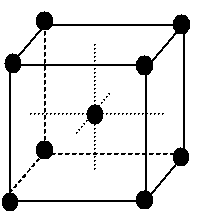
Le chlorure de césium cristallise en formant des réseaux cubiques centrés.

           Cet agencement entraine donc une loi établissant que, malgré toutes les variations possibles des dimensions des faces d’un cristal, l’angle défini par deux faces déterminées ne varie jamais. C’est ce qu’en 1772 le scientifique français Jean-Baptiste Romé de L’Isle avait énoncé de la sorte : " Quelles que soient les dimensions relatives de deux faces déterminées d’un même cristal, elles présentent toujours entre elles le même angle dièdre ".

 

 

        Les ions, ainsi organisés en réseaux, s’agencent dans la matière de façon bien particulière : c’est ce qui donne leur forme géométrique aux cristaux automorphes.

cristaux automorphes et cristaux xénomorphes

Par opposition aux cristaux xénomorphes, les cristaux automorphes ont eu suffisamment d'espace pour obtenir des faces planes, des angles qui se répètent périodiquement, donc une forme géométrique régulière.

          Cette loi mena René Just Haüy, qui s’étonnait alors que plusieurs cristaux de même composition puissent avoir des formes différentes, à une découverte majeure de la cristallographie : les mailles cristallines s’ordonnent selon une brique de base, qui peut ensuite se décliner en d’autres formes. Cette découverte induit donc la notion de clivage : un cristal ne peut se casser que dans certaines directions, conservant une certaine forme, qui est le reflet à notre échelle de cette brique de base.  La déformation du quartz nécessaire à la création d’énergie piézoélectrique dépend aussi de ce facteur.

Des exemples de "briques" formées par les réseaux cristeallins, d'après la découverte de Haüy.

bottom of page